티스토리 뷰

Laplacian Smoothing 복습하다가 발견한 사실인데, math의 graph theory에서 정의하는 laplacian matrix이랑 computer vision과 computer graphics에서 정의하는 laplacian operation이 다른 것 같음. Graph theory에서는 Degree matrix - Adjacency matrix, 즉 difference operation으로 high pass filter이고, Laplacian Smoothing이라는 테크닉과 용어를 사용하는 computer vision/graphics에서는 Adjacency matrix - Degree matrix이다. Input matrix 의 second derivative이기 때문에 얻을 수 있는 formula.
근데 결론부터 말하면 Wikipedia (https://en.wikipedia.org/wiki/Laplacian_matrix) 에 따르면 the graph Laplacian matrix 는 a matrix form of the negative discrete Laplace operator on a graph approximating the negative continuous Laplacian obtained by the finite difference method.
즉 개념상으로는 차이가 없음. 근데 laplacian matrix가 'negative' laplacian operation으로 정의한다 그러면 헷갈릴 수 밖에...


GraphCNN
내친김에 GraphCNN도 복습하자면, spectral graph theory의 graph fourier transform을 이용한 graph filtering을 할 때 이 filter를 learning하는 것이 GraphCNN이다.

Graph Fourier Transform에 따르면 input signal f는 Laplacian Matrix L의 eigenspace에 있고, 즉 L을 eigendecomposition한 후의 eigenvector인 unitary matrix의 column vector의 linear combination으로 inpiut signal f를 표현할 수 있다.

Graph Filtering이라는 건 spatial domain에서의 convolution이 spectral domain에서의 multiplication임을 이용하는 filtering이다. 실제로는 그냥 Matrix multiplication.
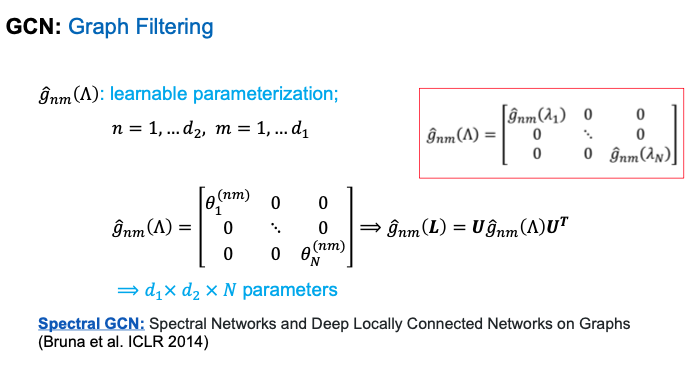

이런 filter의 parameter를 learning하자는 것이 (마치 CNN처럼) 바로 GraphCNN임. 근데 이 graph convolutional filter를 input signal크기만큼 (f: Nxdin) 유지하면 연산량이 N**2이고, 여러 개 쌓으면 N**3, N**4...가 되버리니까, convolution filter 한 장의 paramter를 K개로 parameterization해버림. 이 K는 spatial 한 관점에서는 K-hop near nodes를 정의함. 아무튼 이런 K polynomial paramterization을 하면 Unitary Eigenvector Matrix를 구하기 위해 eigendecomposition을 할 필요도 없어서 효율적임.

근데 이런 high order polynomial 은 non-orthoigonal basis (1, x, x^2, ...)를 가지고 있어서 unstable under perturbation of coefficients. 결국은 하나의 값을 가지기 위해 여러 다른 coefficient 조합이 가능하기 때문에 co-adaptation이 일어나기 쉽고 learning하기 힘들다는 말. 그래서 orthogonal basis를 만드는 Chebnet이 나옴
'Research (연구 관련)' 카테고리의 다른 글
| What is rigid align? (0) | 2024.03.29 |
|---|---|
| What is DDPM and DDIM? (0) | 2024.03.27 |
| What are covariance and correlation? (0) | 2024.03.01 |
| Norm (0) | 2024.02.27 |
| R1 regularization (0) | 2024.02.27 |
- Total
- Today
- Yesterday
- 2d pose
- nohup
- Machine Learning
- Docker
- 비전
- 컴퓨터비젼
- 피트니스
- Virtual Camera
- 헬스
- 인터뷰
- Generative model
- pyrender
- part segmentation
- Interview
- deep learning
- world coordinate
- demo
- focal length
- 문경식
- 머신러닝
- 컴퓨터비전
- Pose2Mesh
- Transformation
- pytorch
- VAE
- camera coordinate
- nerf
- densepose
- 에디톨로지
- spin
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
