Camera Distance-aware Top-down Approach for 3D Multi-person Pose Estimation from a Single RGB Image

2019 ICCV 논문으로 연구실 선배인 경식이형의 논문이다. 이 포스트의 목적은 이 논문의 모듈 중 하나인 'RootNet'에 대해서, 그 중에서도 논문 자체의 contribution보다는, focal length, camera-object distance (depth), per-pixel distance factor에 대해 다룬 내용을 이해하는 것이다.

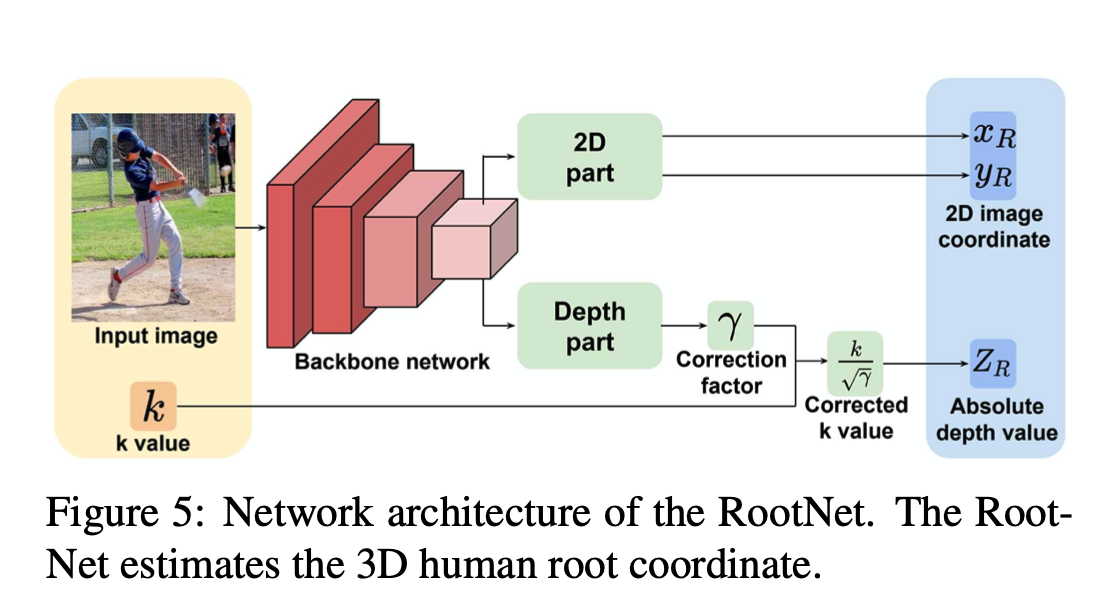
RootNet의 output은 human root joint의 coordinate인 (x,y,Z)이다. x,y는 img coordinate이고, Z는 camera-centered coordinate system 상의 coordiante으로 root joint의 depth다. inference time 때 x,y는 Z를 구한 후에 Z값과 미리 가정한 focal length에 의해 camera-centered coordinate system 상의 coordinate인 (X,Y)로 back project된다. 이 얘기는 마지막에 다시 하겠다. 

root joint의 absolute depth인 Z는 k라는 initial absoulute depth approximation 값 (learning과 상관없음)과 deep learning network의 output으로 depth에 대한 correction factor인 r (gamma)를 곱해 만들어진다. supervision은 root joint의 camera coordinate인 (X,Y,Z)에 행해진다. 이 포스터의 주요 관심사는 이 k로 정의는 다음과 같다.

where alpha x, alpha y, Areal, and Aimg are focal lengths divided by the per-pixel distance factors (pixel) of x- and y-axes, the area of the human in real space (mm2), and image space (pixel2), respectively. k approximates the absolute depth from the camera to the object using the ratio of the actual area and the imaged area of it, given camera parameters. Eq 1 can be easily derived by considering a pinhole camera projection model. The distance d (mm) between the camera and object can be calculated as follows:

즉 d라는 root joint의 approximated depth를 제곱하고 제곱근을 구한 게 k이다. 그렇다면 (2)의 equation이 어떻게 나오는 지 이해해야 하는데, 그전에 pin-hole camera model에서 다음과 같은 식이 성립한다는 것은 다들 이해할 것이다.

The green and blue arrows represent the human root joint centered x and y-axes, respectively. The yellow lines show rays, and c is the hole. d, f, and lsensor are distance between camera and the human root joint (mm), focal length (mm), and the length of human on the image sensor (mm), respectively.

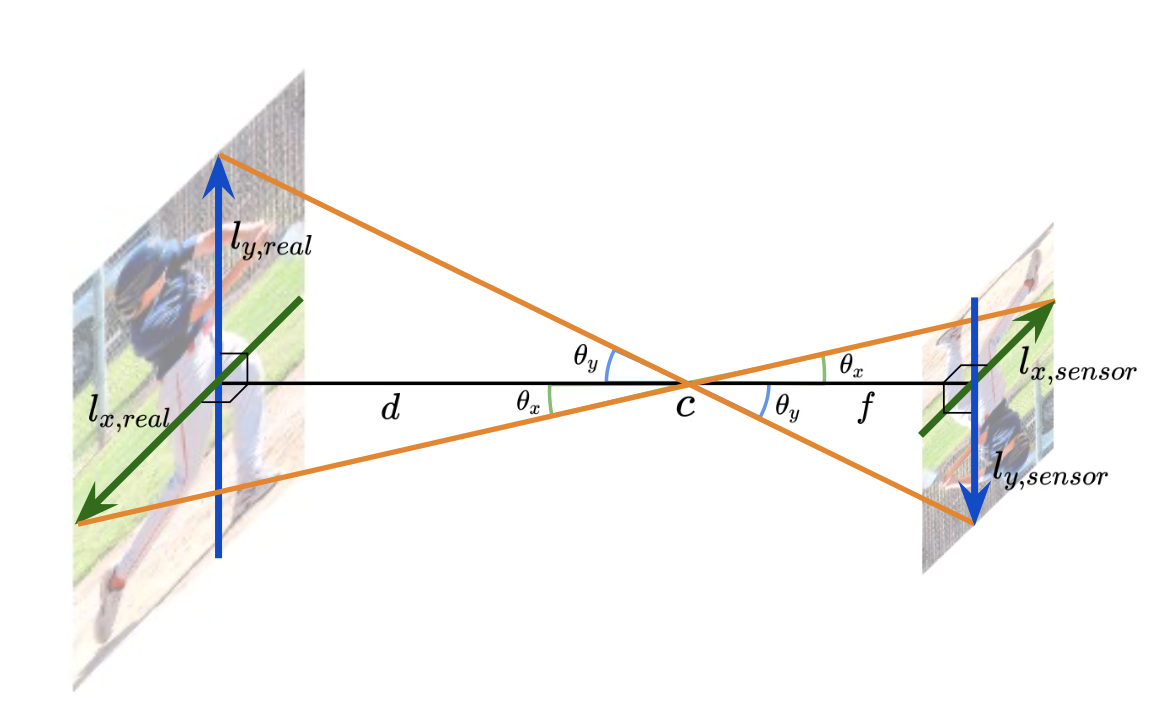
이제 바로 위의 식이 어떻게 (2)으로 바뀌는 지 알려면, alpha x,y 즉 focal length divided by per-pixel distance factor라는 조금 생소한 개념을 이해해야 한다. 여기서 per-pixel distance factor라는 카메라 기종마다 고유한 고정값으로(아마도..), pin-hole camera model을 가정할 때 camera의 image sensor 상에서의 피사체의 단위(mm)를 pixel값으로 바꿔주는 factor의 역수이다. 이 per-pxeil distance factor를 px라 하고 (2)의 equation을 다시 써보면 다음과 같다. 

3번째 항에 대해서 본 논문의 Supplement에서는 fpx 표현해놨는데, f/px로 쓰는게 이해하기 더 직관적이어서 내가 latex으로 다시 썼다.

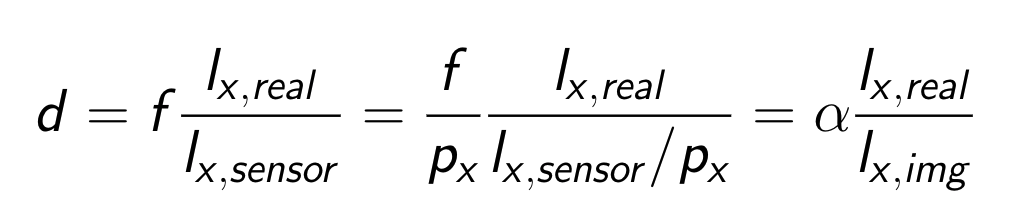
다시 (1)의 equation으로 돌아오면, 본 논문에서는 k를 x-axis에서 근사한 d와 y-axis에서 근사한 d를 곱한 후 제곱근으로 계산했다. 그냥 한 axis에서 구한 d를 쓰거나 두개를 더한 후 나눈 값을 쓰지 않고, 이렇게 한 이유는 아마 (1) equation의 Areal, Aimg 값들이 여러 input에 대해 robust하게 나올 수 있기 때문일 것이다.

위에까지가 이 포스트의 주요 관심사이고, 그렇다면 training때와 inference 때 k의 각 구성 요소인  alpha x, alpha y, Areal, and Aimg는 어떻게 구할까. alpha x,y는  training 때 데이터셋의 카메라 intrisic parameter로부터 구할 수 있고, inference 때는 임의로 설정할 수 있다. 즉 inference 때는 미리 정한 (camera normalized) focal length에 대한 initial depth approximation k를 임의로 설정한다. Aimg는 training, inference 상관없이 input의 bounding box로부터 얻을 수 있고, Areal은 2000mm*2000mm로 고정한다.  Areal 값을 고정하는 로직은, 피사체를 항상 사람으로 가정하기 때문에 평균적인 사람의 크기를 가져다 쓴다는 개념이다. 당연히 이렇게 고정된(constant) Areal값으로부터 나온 k는 에러가 있을 수 밖에 없는데, 바로 Areal이 고정된 값이라는 것에 대한 에러를 correction하는 값(r=gamma)을 learning하는게 바로 RootNet의 목적이다. Areal에 대한 correction factor를 learning할 수 있는 이유는 image feature로부터 그런 정보를 얻을 수 있다는 가정 때문이다. 예를 들어 두 피사체(사람)가 카메라로부터 같은 거리에 있더라도 pose가 다르면 Areal이 다른 데, 사람과 마찬가지로 deep learning network도 image feature를 통해 두 사람의 pose가 다르다는 것을 알 수 있다. 다른 예로 어른과 아이는 Areal이 다른 데, 이 때문에 어른이 카메라로부터 아이보다 더 멀리 있어도 면 Aimg가 더 작거나 비슷해져, 결국 아이보다 더 작거나 비슷한 depth(k)값을 가지게 되는데, deep learning network가 어른/아이 여부를 판별할 수도 있다.

k가 에러를 가질 수 있는 두 예시 상황